「HUSTACM」基础数据结构选讲

本文最后更新于：2022-10-29 23:41:08 UTC+08:00

数据结构

定义

在计算机科学中，数据结构（英语：data structure）是计算机中存储、组织数据的方式。

数据结构意味着接口或封装：一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装。

—— 维基百科 - 数据结构

数据结构是在计算机中存储、组织数据的方式。小到变量、数组，大到线段树、平衡树，都是数据结构。

程序运行离不开数据结构，不同的数据结构又各有优劣，能够处理的问题各不相同，而根据具体问题选取合适的数据结构，可以大大提升程序的效率。所以，学习各种各样的数据结构是很有必要的。

—— OI Wiki - 数据结构

变量与数组

在学语法的时候，我们所用到的变量、数组，就是一种最基本的数据结构。

定义变量时，系统会分配一块内存来存储这个变量对应的值。

而数组就是由相同类型的元素（比如 int、double 类型等）的集合所组成的数据结构，分配一块连续的内存来存储。利用元素的索引（数组的下标）可以计算出该元素对应的存储地址，直接获取数组的值。

数组的特点：可随机访问，可以用下标读取、修改任意一个元素。

int arr[100];
arr[0] = 1;
arr[99] = 100;
printf("%d\n", arr[99]);

为什么数组的下标从 0 开始？

因为数组的下标本质上是内存地址的偏移量。

1	`printf("%d = %d\n", arr + 1, &arr[1]); // 两个地址相等`

栈

只能对一端（栈顶）进行插入（入栈）、删除（出栈）操作。

栈的特点：先进后出，不可随机访问。

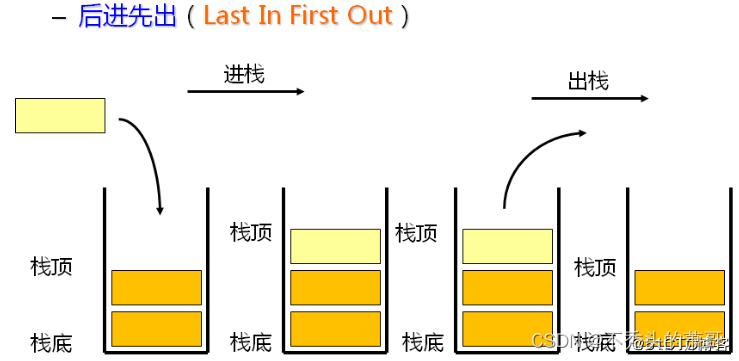
用数组模拟栈：

int st[N]; // 定义栈
int tp;    // 定义栈顶下标，0 表示栈里没有元素。

void push(int x) { // 入栈
  st[++tp] = x;
}

int pop() { // 出栈，并返回被弹出的栈顶元素
  if (!tp) return -1; // 栈为空
  return st[tp--];
}

st[tp] // 取栈顶元素

例题：Luogu P5788 【模板】单调栈

给一个长度为 \(n\) 的序列 \(a\) ，对于每个 \(1 \leq i \leq n\) ，求出第一个大于元素 \(a_i\) 的值的下标。

单调栈：始终保持从栈底到栈顶（非严格）单调递增或递减的栈。

按照样例手动模拟单调栈：

1 2	`5 1 4 2 3 5`

对于本题，我们使用从栈底到栈顶单调递减的栈，枚举 \(i\) ，对于每一个元素都需要入栈，入栈时，需要判断栈顶是否小于当前元素，如果是则需要弹出栈顶元素，并记录栈顶元素对应下标的答案。

st: 1
st: 4 // 当 4 入栈时，我们发现栈中已有元素 1 比 4 小，所以需要弹出 1 并记录 1 的答案(2)（遇到了第一个比他大的元素）
st: 4 2 // 2 入栈时，没有遇到比他小的元素
st: 4 3 // 3 入栈时把 2 弹出，并记录 2 所在位置的答案(4)
st: 5 // 5 入栈时连续遇到了两个比他小的元素，都需要弹出并记录 4 和 3 对应位置的答案(5)

最终栈只剩下 5 这个元素，而序列已经结束了，说明该序列已经没有比 5 大的元素了。

按照上面流程，我们可以得到答案：

1	`2 5 4 5 0`

代码：

int st[N]; // 这里栈存的是下标，方便直接存储答案
int tp = 0;
int ans[N];

for (int i = 1; i <= n; i++) {
  while (tp && a[st[tp]] < a[i]) {
    ans[st[tp]] = i;
    tp--;
  }
  st[++tp] = i;
}

【拓展】C++ STL 中的 std::stack

#include <stack>

std::stack<int> s;
s.push(1); // 入栈
s.pop();   // 出栈
s.top();   // 取栈顶元素
s.empty(); // 查询栈是否为空
s.size();  // 查询栈元素数量

队列

对两端都可以操作，一端插入（进队），一端删除（出队）。

队列的特点：先进先出，不可随机访问。

用数组模拟队列：

int ql = 1, qr = 0; // 队首和队尾下标
int q[N];

void push(int x) { // 入队
  q[++qr] = x;
}

int pop() { // 出队
  if (ql > qr) return -1; // 队列为空
  return q[ql++];
}

q[ql] // 取队首元素
q[qr] // 取队尾元素

双端队列：队首和队尾均可以插入和删除元素。

例题：Luogu P1886 滑动窗口 /【模板】单调队列

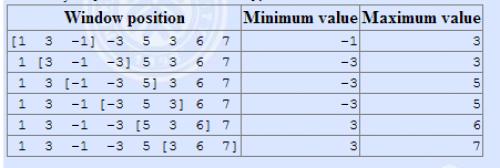
有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

类似单调栈，这里采用单调队列（双端）。

现在我们只考虑求出窗口中的最大值。最小值同理可以类比。

如果这个窗口无限长，那么相当于前面说到的单调栈，栈底元素即为窗口中的最大值。

但是窗口大小限制为 \(k\) ，我们就需要在将第 \(i\) 个元素入队之前把第 \(i-k\) 个元素出队，否则就超出了窗口的大小。

求最大值，我们采用（非严格）单调递减的队列。

8 3
1 3 -1 -3 -5 3 6 7

q: 1
q: 3 // 3 比 1 大，需要把 1 出队
q: 3 -1 // 此时可以发现窗口大小已经是 3 ，所以可以开始记录每个窗口的答案。第一个窗口的答案就是队首元素：3
q: 3 -1 -3
q: -1 -3 -5 // 到这时可以发现原本队首的 3 元素已经超出了窗口的大小(3) ，所以需要将 3 出队，才能入队 5
q: 3 // 3 比之前的所有数都大，所以将前面的数全部出队
q: 6
q: 7

代码（仅最大值部分）：

int ql = 1, qr = 0;
int q[N]; // 这里同样记录的是下标
int ans[N];

for (int i = 1; i <= n; i++) {
  if (ql <= qr && q[ql] <= i - k) ++ql;
  while (ql <= qr && q[qr] < a[i]) --qr;
  q[++qr] = i;
  if (i >= k) ans[i - k + 1] = q[ql];
}

最小值部分同理，可以用单调递增的队列求解，留给各位自行思考。

【拓展】C++ STL 中的 std::queue 和 std::deque

#include <queue>

std::queue<int> q;
q.push();  // 入队
q.pop();   // 出队
q.front(); // 取队首元素
q.back();  // 取队尾元素
q.empty(); // 判断队列是否为空
q.size();  // 取队列元素数量

#include <deque>

std::deque<int> d;
d.push_back();
d.pop_back();
d.push_front();
d.pop_front();
d.front();
d.back();
d.empty();
d.size();

链表

由若干节点组成的线性表，每一个节点存储数据和下一个节点的指针。

链表的特点：插入、删除元素复杂度 \(\Theta (1)\) ，查找元素复杂度 \(\Theta (n)\) 。

双向链表：每个节点都存储上一个节点和下一个节点的指针。

链表的插入、删除元素，见：https://oiwiki.org/ds/linked-list/

例题：Luogu P1160 队列安排

一个学校里老师要将班上 \(N\) 个同学排成一列，同学被编号为 \(1\sim N\)，他采取如下的方法：

先将 \(1\) 号同学安排进队列，这时队列中只有他一个人；

\(2-N\) 号同学依次入列，编号为 \(i\) 的同学入列方式为：老师指定编号为 \(i\) 的同学站在编号为 \(1\sim(i-1)\) 中某位同学（即之前已经入列的同学）的左边或右边；

从队列中去掉 \(M(M<N)\) 个同学，其他同学位置顺序不变。

在所有同学按照上述方法队列排列完毕后，老师想知道从左到右所有同学的编号。

第 2 步中老师将学生插入到原队列的某个位置里，对应链表的插入操作。如果我们用数组来维护这个队列，那么每次插入都需要把插入的位置的后面所有同学向后移动一位，这样每次插入的复杂度是 \(\Theta (n)\) 的。如果使用双向链表，我们只需要新建一个节点，并修改插入位置前后的编号信息（指向新建的节点）即可。

删除操作，同样的我们只需要修改删除位置前后节点的编号信息（指向被删除节点后面的节点）即可。

用数组模拟双向链表，代码：

int pre[N]; // 链表中当前节点指向上一个节点的编号信息
int nxt[N]; // 链表中当前节点指向下一个节点的编号信息
int h = 1;  // 链表头部编号

void insert(int i, int p) { // 编号为 i 的人放到编号为 p 的人之后
  int b = nxt[p]; // 原来在编号为 p 的人后面的人的编号
  nxt[p] = i;
  nxt[i] = p;
  if (b) pre[b] = i; // 需要判断编号为 p 的人是否为链表末尾
  pre[i] = p;
}

void del(int i) { // 从链表中移除编号为 i 的人
  int pr = pre[i], nx = nxt[i];
  if (pr) nxt[pr] = nx; // 判断编号为 i 的人是否为链表头部
  if (nx) pre[nx] = pr; // 判断编号为 i 的人是否为链表末尾
  if (i == h) h = nx;
}

树

由 \(n\) 个节点组成的具有层次关系的集合；由 \(n\) 个点 \(n-1\) 条边构成的无向图。

树有以下特点：

每个节点都只有有限个子节点或无子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树；
树里面没有环路。

树有一些基本概念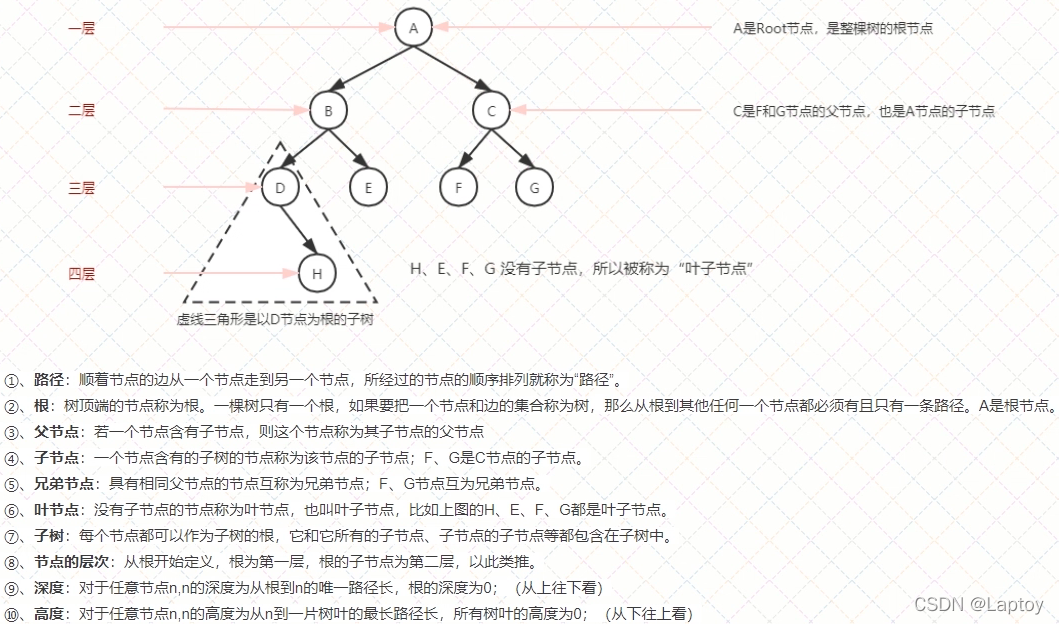：树的一些常用概念

森林：若干棵互不相交的树的集合。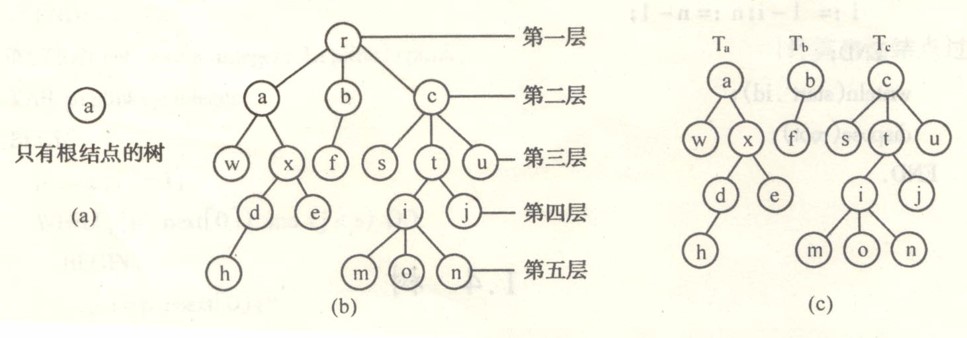

如果继续学习，之后的堆、并查集、树状数组、线段树、平衡树等数据结构，还有基于树的 DP、启发式合并等都离不开树的支持。

有关二叉树的一些概念：

二叉树：每个节点最多含有两个子树的树称为二叉树；
完全二叉树：对于一棵二叉树，假设其深度为 \(d\ (d > 1)\) 。除了第 \(d\) 层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；
满二叉树：所有叶节点都在最底层的完全二叉树（有争议）。

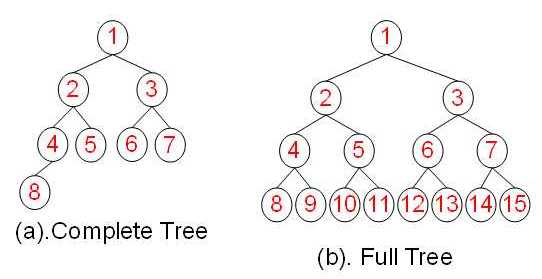
二叉树的一些性质：

二叉树第 \(i\) 层最多有 \(2^{i-1}\) 个节点。
在深度为 \(d\ (d > 1)\) 的二叉树中最多有 \(2^{d} - 1\) 个节点（满二叉树）。
具有 \(n\) 个节点的完全二叉树深度为 \(\lfloor \log_2 n \rfloor + 1\) 。
编号性质：

二叉树的遍历：前序、中序、后序遍历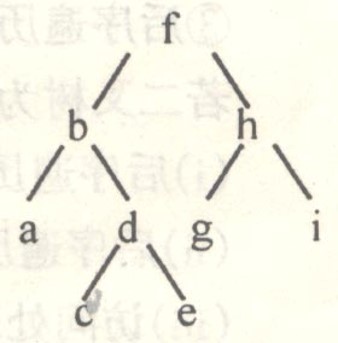示例树

前序遍历：根节点 -> 左子树 -> 右子树
中序遍历：左子树 -> 根节点 -> 右子树
前序遍历：左子树 -> 右子树 -> 根节点

对于每个子树采取相同的遍历方式。

对于如图所示的树： - 前序遍历：f badce hgi - 中序遍历：abcde f ghi - 后序遍历：acedb gih f

【拓展】树的遍历的实现：深度优先搜索 (dfs)

堆

堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。

每个节点的键值都大于等于其父亲键值的堆叫做小根堆，否则叫做大根堆。

二叉堆：是一棵完全二叉树。

插入、删除操作：见 https://oiwiki.org/ds/binary-heap/

例题：堆排序

void max_heapify(int arr[], int start, int end) {
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) {
        if (son + 1 <= end && arr[son] < arr[son + 1])
            son++;
        if (arr[dad] > arr[son])
            return;
        else {
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort() {
    for (int i = n / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, n - 1);
    for (int i = n - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}